PRY: Difference between revisions
| (13 intermediate revisions by the same user not shown) | |||
| Line 16: | Line 16: | ||
In a next step, a MySQL database will be coupled to PRY 3.0 beta that permits translation of CowSense (TM by Midwest Microsystems) export data into demographic input parameters for PRY. | In a next step, a MySQL database will be coupled to PRY 3.0 beta that permits translation of CowSense (TM by Midwest Microsystems) export data into demographic input parameters for PRY. | ||
==DIC - Demographic Program Input Constants== | |||
'''''Purpose of DIC''''' | |||
PRY provides an interactive routine for entering demographic parameters or inherent fitness traits. These are: survival rates, selective culling rates, | |||
age at first parturition, parturition interval and litter size. This routine is referred to as DIC (Demographic Program Input Constants). At every step | |||
of parameter entry, checks are carried out, error messages displayed and only consistent values accepted to avoid crashing of the simulation and | |||
derivation routines. Specification of age groups, rates and histograms is flexible. After entry, the parameters are formatted and saved to a work | |||
file from which they are later retrieved by the simulation and derivation routines. | |||
'''''Survival Rates''''' | |||
A survival rate is the fraction of animals still present at the end of a time interval if no living animal were disposed of. Such a rate represents an inherent potential and can be specified even for age classes which, in practice, are not at all represented because animals are culled before that age. Survival rates observed under a specific culling pattern may well differ from the survival rates to be specified as inherent demographic parameters. Survival rates can be specified for arbitrary age classes as either an annual rate or as a fraction surviving to the end of the specified interval. Such an interval or age class is defined in terms of a starting week or month of age and an ending week or month. The period covered can be more or less 8than a year. | |||
Animals surviving to the ’biological’ maximum age specified, are assumed to be lost, rather than culled at the last time-step. However, animals | |||
surviving to a cull-for-age threshold lower than the ’biological’age limit,are assumed to be culled. | |||
If only one survival rate per sex is specified, the age group then includes all ages from the first month or week of age up to the highest possible age. | |||
A maximum of 14 age groups can be defined. Male and female survival rates may be the same. However, age group boundaries and corresponding | |||
rates can also be defined for each sex separately. | |||
Losses and culls in breeding females are not always clearly distinguishable. Emergency slaughter is an anticipated mortality or a cull, depending on the value of deadweight. Youngstock is never disposed of on voluntary grounds unless it has reached ’marketing’ age. Therefore, forced culls in youngstock are to be aggregated with losses. The value of deadweight can be adjusted correspondingly, to reflect an expected average of real losses of low salvage value and forced cullings of high salvage value. | |||
'''''SCRAP - Selective culling rates in breeding females''''' | |||
In practice, breeding females which have not yet reached the cull-for-age threshold are not culled on a yearly basis as assumed in most livestock | |||
productivity models. Rather, a certain fraction per parity can be expected to fail to conceive or pose problems like low yield or poor health. Culls | |||
based on problems like low yield or conformation are not really forced ones like culls for failure-to-conceive or poor health. Both forced and arbitrary | |||
culls of breeding females do, however, have the same effect in terms of population dynamics. That is why they are treated alike and aggregated | |||
into a ’selective culling rate per parity’ of breeding females (SCRAP-rate). For example, if the ’true’ sterility rate is 0.05 and the rate of low yielders is 0.10, the SCRAP-rate to be entered would be 0.15, which is the rounded value of the conditional probability: | |||
1–(1–0.10) (1–0.05) = 0.145 | |||
assuming that an animal’s yield level is independent of its reproductive performance. | |||
The SCRAP-rate should not include the fraction of lost animals, i.e., forced culls with a low enough salvage value to be aggregated with mortalities. The distinction is often made between involuntary and voluntary culls. The best way to avoid confusion is probably to first think in terms of animal losses, on the one hand, and culls on the other. Then, culls are further differentiated according to whether they are forced or arbitrary. It depends on the context of the modelling exercise how ’exits’ are partitioned among these categories. | |||
’Sterile’ breeding females are assumed to be recognized as such only when a parturition is overdue. In the case of ’sterile’ nulliparous breeding females this means that they are culled at an age when practically all ’fertile’ age-mates have given birth. In the case of ’sterile’ primi- and multiparous animals it means that they are culled when fertile age-mates have nearly all given birth again. Animals with a low yield and animals of poor health are, like ’steriles’ likely to be culled only after weaning or at the end of a lactation when the parturition interval, statistically speaking, tends towards its end. Therefore, selective culls, both for failure-to-conceive and other ’problems’, are treated alike and assumed to take place shortly before the next parturition is due. | |||
In conclusion, the compound rate of selective culling per parity is to give the fraction of breeding females in an age group which are earmarked to be culled when a next (or the first) parturition is ’overdue’. When culling actually takes place is detailed in the sections on the animal population emulator and the stationary-state demographic model, respectively. Both routines use the same parameter of a SCRAP-rate. The SCRAP-rate gives a fraction per parity. However, age dependency is taken into account by varying the rate by age. A minimum of two age groups and a maximum of 14 can be defined. The SCRAP-rate of the first age group is applied to nulliparous breeding females. The other rates are applied to those breeding females having a parturition in the respective age group. Like survival rates, SCRAP-rates are inherent parameters. An ’ear-marked’ breeding female can die or reach the cull-for-age threshold before ’scrapping’ actually takes place towards the expected end of the parturition interval. | |||
'''''Age at first parturition''''' | |||
The age at first parturition is specified in weeks or months. It is given as a frequency distribution. The special case of a histogram with only one column represents a statistical population with a mean but zero variance. As the column heights of the histogram are edited, the mean and standard deviation are calculated and displayed by the program. The histogram can be composed of up to 14 columns. The height of each column is entered using an arbitrary scale. It is not essential but preferable to specify a histogram with more than one column. With only one column very fluctuating population sizes will result for the dynamic model due to an effect of synchronisation. A multi-column histogram, even if it is the very crude approximation of a rectangular distribution, will desynchronize births. Consequently, simulated population sizes and structures become more continuous. | |||
'''''Parturition interval''''' | |||
Like age at first parturition, the parturition interval is specified as a histogram. The remarks of the preceding paragraph concerning age at first parturition apply. The parturition interval represents only a partial aspect of reproductive fitness. In the model, it is complemented by the SCRAPrate which normally represents an age-dependent sterility rate. | |||
'''''Litter size''''' | |||
Litter size is specified as the histogram of number-of-young per litter. An average litter size which is not an integer number cannot be specified as a | |||
single-column histogram. A multiplecolumn histogram with integer class means must be defined so as to get an appropriate population mean. This weighted average is continuously updated and displayed as the histogram of litter size is edited. Even when average litter size can be given as an integer value, it is preferable to enter a multiple-column histogram, in order to smoothen fluctuations of population size in runs of the dynamic model. | |||
==APE - Animal Population Emulator== | ==APE - Animal Population Emulator== | ||
'''''Purpose of APE''''' | |||
The Animal Population Emulator (APE) stochastically simulates births, culls and losses in a seed herd or flock of finite size (¡1000). APE can only simulate population dynamics but not productivity proper. The procedure can be used to analyse population structure and animal offtake over time. This can be a useful complement to stationary-state demography, especially with regard to financial discounting exercises. APE is an ’electronic’ population system. Whether it can model animal populations depends on the objectives. Many aspects of livestock populations are idealised or abstracted from. For example, litter size is assumed to be the same in different parities. Culling regime and fitness traits remain the same over time. Due to the stochastic variation of survival, sex-ratio, age at first parturition, calving interval, litter size and culling, every simulation run will give different results. Apart from being a dynamic and stochastic system, APE models reproduction, losses and culls in much the same way as does the deterministic Stationary-state Animal Demographic Model (SAM, see below). Consequently, APE can be used to validate SAM and vice versa. | |||
'''''Index card population''''' | |||
An individual animal is represented by a file record whose entries represent the sex of the animal, its age in time units of weeks or months, an identification number, the time elapsed since the last parturition (if applicable), and the number of weeks or months to wait until the next parturition, provided the animal survives. Records of females ’earmarked’ for selective culling, indicate that there is no next parturition even if the animal survives. There are no entries regarding yields. | |||
At consecutive time-steps (weeks or months) each survivor’s record is either eliminated or maintained. At the beginning of a time-step, the program looks up the survival probability for the week or month corresponding to the animal’s age and decides over survival or loss of the animal on the basis of a random number. If a female survives, the program looks up whether a parturition is due. If so, litter size is determined by generating a random integer number from a distribution as specified by the histogram of litter size. The sex of each animal born is randomly determined with an expected frequency of males of 50 %. For newborn females the SCRAPrate of nulliparous females randomly determines whether the animal is to have a first parturition. If it is not to be sterile, the number of time units to wait until the animal’s first parturition (if it survives), is drawn from a frequency distribution defined by the histogram of age at first parturition. | |||
For the females having given birth, the SCRAP-rate specified for their agegroup randomly determines whether a next parturition is expected. If so, the number of time units to wait is drawn from a frequency distribution defined by the histogram of the parturition interval. After thus simulating mortalities and reproduction, culling decisions are taken. APE offers seven different options which are explained below in the section on the simulation plan. Before a next time-step starts, the age entries of the survivors are updated. Cycles are repeated until the population dies out or grows too big (>1000), until run-time is out or until the required number of repetitions and of time-steps per repetion are done. A repetition resumes simulation starting off again with the same seed herd or flock. At the end of the simulation experiment the surviving population of animal records is saved in a work file. This population of survivors can be used as a seed herd or flock in subsequent simulation runs. | |||
'''''Seed herd or flock''''' | |||
APE needs a seed herd or flock. It can consist of up to 1000 animals. When the seed population is entered the sex of the animal and its age have to be | |||
specified. Nulliparous females have to be identified as such. For primi- or multiparous females a specification of the time elapsed since their last parturition is required. Animals having identical entries are entered as multiple copies of a record. | |||
After at least one simulation run, a work file is saved containing the population of survivors from the final time-step of the completed simulation experiment. This population of records contains the same entries as the records of a seed herd or flock. Such a population of survivors can therefore serve as a seed population of a subsequent simulation experiment. This 13feature can be used to vary parameters over time. | |||
The population of survivors can be edited before it is used as a seed population. Editing can consist of a random reduction of population size, or a random increase. It is also possible to ’manually’ select animals and eliminate them from the population. Culling patterns not covered by the options offered can be simulated step-wise, by loading the (ASCII) file of survivors into a spreadsheet or database package and by using standard procedures like sorting, selecting and deleting, to eliminate groups of records before saving the edited file back to the work file containing the seed population. The specification, in that file, of the number of records it contains, has to be updated before saving. The cropped population is then left to develop over one or more time-steps before it is cropped again. | |||
'''''Simulation plan''''' | |||
Before the seed population can be developed, a work file containing a simulation plan has to be edited. The simulation plan specifies an experimental design and the culling pattern to which the seed population is to be subjected. The experimental design specifies whether the seed population is a previously entered one, or whether it consists of survivors from a preceding run. It also decides on the number of repetitions to be run, the number of time-steps to be simulated per repetition and the length in number of time-steps of an accounting interval, i.e., the period over which the numbers of culls, deaths, births and survivors per animal category are to be cumulated before sub-totals are saved. In addition, the program prompts | |||
for a maximum run-time after which the experiment is stopped if it is not yet completed. As a further condition to stop a repetition, the maximum | |||
population size has to be specified. | |||
To define the culling pattern, one of seven optional practices has to be selected: | |||
# No culling, only natural deaths until target population size is reached or run-time is out | |||
# Culling only when target population size is exceeded | |||
# Constant offtake rate whether the population grows or decreases | |||
# Allowance for a constant rate of increase in population size | |||
# Immediate disposal of newborn males; all females are bred until they are culled for sterility or lost | |||
# All newborn females become potential breeders culled at an age threshold or when sterile | |||
# A fixed number of male and female breeding animals is kept whose age exceeds the youngstock disposal age but is below a cull-for-age threshold | |||
For some of these options (2, 3 and 4), additional specifications are prompted. When one or more animals have to be culled, a decision has to be taken as to which animal(s) from among the survivors has to be eliminated. APE simulates four optional strategies: | |||
# Each animal’s entries are displayed for a culling decision. | |||
# A culling rank is determined for each animal. Old males have highest culling priority. Females are ranked according to ’fertility’ (i.e., time units that have elapsed since the last parturition) and age. ’Sterileyoung’ is culled before ’fertile-old’. During culling, minimum requirements are considered. If no sufficiently old or ’sufficiently sterile’ animals are left, males are eliminated starting with the oldest ones. When no males are left, females which in principle are too young or too ’fertile’ are culled according to the established ranking. | |||
# Ranks are established similarly. However, ’fertile-old’ females are culled before ’sterile-young’ females. | |||
# Basic pattern as under option 2. However, when no ’sterile’ females are left, sexually immmature ones with minimum age requirement are culled. After elimination of males, immature females are culled in reverse order of ages, i.e., youngest first. | |||
Minimum requirements sometimes are conflicting and cannot all at the same time be taken into account when many animals have to be culled in order to keep population size constant. The number of violations are recorded with the results. Culling option 7 avoids this kind of conflict and is the most relevant in a stockbreeding context. | |||
'''''Demograms''''' | |||
Over the length of the ’accounting’ period specified in the experimental design, losses and culls are cumulated for the six animal categories specific to APE, i.e., adult and subadult males, adult and subadult females with either no or at least one parturition. The sub-totals per category are saved in a work file for successive ’accounting intervals’ within a repetition. Annualized rates of births, culls and losses are shown, as well as the population growth rate. The base for these rates is not population size at the start or the end of the ’accounting’ interval but, rather, the average size over the length of the ’accounting’ interval. Population structure is expressed as the number of animals still alive at the end of a period in each of the six animal categories. | |||
Results are saved in an ASCII work file. If an experimental design specifies 3 repetitions with 5 periods each, the work file will contain 15 records at the end of the completed experiment. In addition to the 15 data records the work file contains a record with the abbreviated variable names or column headers. For graphical or statistical analyses, variable names and data from the work file of results have to be imported into a spreadsheet. Within the spreadsheet, the results can be sorted, aggregated or plotted, and statistics can be calculated. | |||
A standardized form of presenting population dynamics has been suggested and referred to as a demogram. A representative demogram is reproduced in Figure 3 (will be inserted) which is an example of how simulation results can be presented in order to reveal the development over time of population | |||
size, population structure, animal offtake, offtake composition and demographic rates. | |||
==SAM - Stationary-State Animal Demographic Model== | ==SAM - Stationary-State Animal Demographic Model== | ||
'''''Purpose of SAM''''' | |||
The Stationary-State Animal Demographic Model (SAM) derives population structure, animal offtake, a number of life expectancies and the potential rate of increase of population size for an infinitely large population at the stationary-state equilibrium of the imposed culling regime. Growth is zero because females not needed to replace lost or culled breeding females, are ’fattened’, or rather, ’sized’. The program automatically varies disposal ages to indicate how this affects stationary-state demography. Disposal age of female surplus and male youngstock, respectively, is varied in increments of one quarter of the age at first parturition. Simultaneously, the cull-for-age threshold of breeding females is varied in increments of the parturition interval. The effect of varying SCRAP-rates can be analysed by running SAM with previously modified rates. | |||
'''''Life and fecundity tables''''' | |||
Stationary-state demography is derived from life, fecundity and auxiliary tables generated according to actuarial principles applying elementary probabilistic calculations. The required tables are automatically generated by SAM on the basis of the demographic input constants, i.e., the inherent fitness traits of a population. A life table is a vector of weekly, monthly or annual survival rates. A fecundity table gives the number of young produced per surviving female at various ages. The set of vectors as generated by SAM is referred to as actuarial table. Table 10 represents such a set derived from the fitness traits in Table 9. The population could be a laboratory strain of not very viable guinea pigs. The actual values used are quite irrelevant because they only serve to exemplify the actuarial method. | |||
TABLE 9 - Fitness traits assumed for a hypothetical example of laboratory guinea pigs | |||
''comming soon'' | |||
TABLE 10 Actuarial table generated generated for the example of laboratory guinea-pigs | |||
''comming soon'' | |||
'''''Life expectancies''''' | |||
Table 11 shows some of the life expectancies which SAM calculates for the example of guineapigs. Thecull-for-age threshold of breeding females is 18 or 14 months. The upper level rep- resents the ’biological’ maximum age. | |||
Breeding females are only culled when sterility is recognized but otherwise they are kept until they are lost. The few who might reach the maximum age die. At a cull-for-age threshold of 14 months the population’s viability is reduced, which is reflected by the reduction from 1913% of the potential rate of increase of population size (see below). A further reduction of the cull-for-age threshold from 14 to 10 months makes the population unviable and a stationarystate is not possible at this level. | |||
'''''Potential rate of increase of population size''''' | |||
A stationary state can only exist when the population is sufficiently viable to maintain itself despite losses and culls. A measure of population viability is the potential rate of increase of population size. It reflects the rate of increase expected when culling of fertile females is completely suppressed and when the population has established an equilibrium with regard to structure and steadiness of growth. The derivation of this rate from the actuarial table is not trivial. It requires an iterative solution of Lotka’s equation. The program needs only about four to six iteration 18 cycles to find the approximate rate for which the right-hand side of Lotka’s equation deviates by less than 0.0001 from the expectation of unity. | |||
The potential rate of increase of population size may be found to be negative. This means that the closed population is bound to die out gradually. This can be caused by too heavy culling of breeding females (SCRAP-rate), or because the cull-for-age threshold is too low, or because of weak inherent fitness. In such cases further derivations have to be suppressed because a stationary-state is not possible. Thus, the calculation of the potential rate of increase of population size is a safeguard against unrealistic assumptions and serves as a consistency check with regard to assumed fitness values and imposed culling pressure. | |||
TABLE 11 - Life expectancies under two regimes with different cull-for-age thresholds for breeding females of laboratory guinea-pigs | |||
No culling for age (threshold set to maximum biological age) | |||
* Life expectancy at birth (years of age) of breeding females : 0.8230 | |||
* Life expectancy at birth (no. of parturitions) of bdg. fems. : 1.1416 | |||
* Number of female surplus per newborn female : 0.1416 | |||
* Avg. age at parturition in years (gen.int. for breeding females): 0.6684 | |||
* Potential annual rate of increase of population size (%) : 19.40 | |||
* Selective culls in % of breeding female offtake : 100.00 | |||
* Cullings for old age in % of bdg female offtake : 0.00 item Breeding | |||
* Female offtake / Breeding Female losses : 0.40 | |||
* Cull-for-age threshold set to 14 months | |||
*Life expectancy at birth (years of age) of breeding females : 0.7916 | |||
*Life expectancy at birth (no. of parturitions) of bdg. fems. : 1.0955 | |||
* Number of surplus females per newborn female : 0.0955 | |||
* Avg. age at parturition in years (gen.int. for breeding females): 0.6410 | |||
* Potential annual rate of increase of population size (%) : 13.47 | |||
* Selective culls in % of breeding female offtake : 75.24 | |||
* Cullings for old age in % of bdg female offtake : 24.76 | |||
* Breeding Female offtake / Breeding Female losses : 0.66 | |||
TABLE 12 - Offtake rate, composition and population structure under two regimes with different cull-for-age thresholds for the example of laboratory guinea-pigs | |||
No culling for age (threshold set to maximum biological age): | |||
''comming soon'' | |||
'''''Offtake rate and population structure''''' | |||
Table 12 shows that the cull-for-age threshold of 14 months increases all offtake rates relative to those at 18 months. At each cull-for-age threshold, different combinations of disposal ages of youngstock produce different offtake rates, offtake compositions and population structures. An increased offtake rate is, of course, not an advantage in itself. Other offtakes, their unit values and the feed requirement involved have to be taken into account. This is accomplished by the program components FOC and BOI described in later sections. | |||
==PIC - Produce-Related Program Input Constants== | ==PIC - Produce-Related Program Input Constants== | ||
==FOC - Find optimal Culling Ages== | ==FOC - Find optimal Culling Ages== | ||
| Line 26: | Line 214: | ||
=The Algorithms= | =The Algorithms= | ||
==Hardware Requirements | =Before you Start= | ||
'''Hardware Requirements''' | |||
| Line 61: | Line 250: | ||
Unless you are a developer or require Modules from the original DOS Software, you most proably want to use the 3.x Version of the Software, provided as an installable Windows App. Download of other Versions below | Unless you are a developer or require Modules from the original DOS Software, you most proably want to use the 3.x Version of the Software, provided as an installable Windows App. Download of other Versions below | ||
'''PRY 3.x''' | |||
| Line 76: | Line 265: | ||
Access previous Versions of PRY | '''Access previous Versions of PRY ''' | ||
*[[PRY_3#Version_History|Version History]] | *[[PRY_3#Version_History|Version History]] | ||
| Line 82: | Line 271: | ||
*[[PRY_1#Download|Download PRY 1.x]] | *[[PRY_1#Download|Download PRY 1.x]] | ||
=Installation Manual= | |||
| Line 142: | Line 323: | ||
If you encounter any problem with installing PRY on your computer, you may ask for [[Contact|support]] | If you encounter any problem with installing PRY on your computer, you may ask for [[Contact|support]] | ||
=User Manual= | |||
For other Versions see User Guide here | |||
;[[PRY_2#User_Guide|Version 2.x]] : PRY realized as Modules in an Excel sheet | |||
;[[PRY_1#User_Guide|Version 1.x]] : The original PRY, a DOS console Program | |||
==Model Input Parameters== | ==Model Input Parameters== | ||
| Line 181: | Line 373: | ||
|''Evaluation of cropping strategies in game ranching using a livestock productivity model'' | |''Evaluation of cropping strategies in game ranching using a livestock productivity model'' | ||
|http://dx.doi.org/10.1016/0921-4488(91)90124-9 | |http://dx.doi.org/10.1016/0921-4488(91)90124-9 | ||
|Game | |||
|+ | |||
|Fink H. and Baptist R. | |||
|1992 | |||
|Better feeding for improved production - FAO Series | |||
|''Herd dynamics modelling applied to a venison ranch in Kenya'' | |||
|http://www.fao.org/docrep/u8750t/u8750T04.htm | |||
|Game | |||
|+ | |+ | ||
|Anonymous | |Anonymous | ||
| Line 219: | Line 419: | ||
|+ | |+ | ||
| | |Dickhoefer et al. | ||
| | |2012 | ||
| | |Agricultural Systems 110,C, 131-141 | ||
| | |Modeling herd development and revenues from Jabal Akhdar goats under current and intensified management | ||
| | |http://www.sciencedirect.com/science/article/pii/S0308521X12000583 | ||
| | |Goat | ||
|+ | |+ | ||
|Riedel | |Riedel et al. | ||
| | |2014 | ||
| | |Livestock Science, 160, 151-162 | ||
| | |The productivity of traditional smallholder pig production and possible improvement strategies in Xishuangbanna, South Western China | ||
| | |http://www.livestockscience.com/article/S1871-1413%2813%2900502-7/abstract | ||
|Pigs | |Pigs | ||
|+ | |+ | ||
Latest revision as of 16:45, 7 September 2016
What is PRY
PRY is a bio-economic livestock herd/population model developed by Dr. habil. Richard Baptist (formerly of the University of Nairobi and the University of Hohenheim) in 1988. PRY is a species independent, livestock-driven, herd model, which combines deterministic and stochastic procedures and allows for assessing herd/population productivity, simulating herd/population development, comparing productivity between livestock systems and management strategies within livestock systems.
PRY derives a productivity index (PI) "total output value/dry matter intake (TOV/DMI)" as a measure of overall productivity of an animal production system. Dry matter intake is chosen as denominator in this index because feed is considered the most limiting production asset as it generally accounts for the major part of production costs and is the main input factor in extensive animal husbandry systems.
PRY in its original DOS based version consists of six single components or modules (DIC, PIC, SAM, FOC, BOI, APE). Demographic input parameters are entered and stored in DIC. Produce-related input parameters are entered and stored in PIC. Deterministic modelling components SAM, FOC, and BOI derive population structure, numeric offtake, life expectancies and potential rate of increase of population for an infinitely large, closed equilibrium population (a population at steady state) from the DIC parameters. Total offtake value per dry matter intake for different disposal strategies is derived adding information from the PIC parameters, thus the model permits to find an optimal culling strategy (FOC). With a specific culling regime specified, a detailed breakdowns of offtake and intake (BOI) can be derived. The stochastic animal population emulator APE permits the simulation of herd/population development over time.
PRY was further developed by Dr. Richard Baptist into an MS Excel add-in named HerdLife. HerdLife combined the different modules above and eased handling of the model, particularly parameter input as well as display and storage routines.
In a current effort encouraged by the model author, PRY / HerdLife will be linked to external data sources – i.e. spreadsheet or database applications often used in research projects as well as livestock management programmes such as CowSense (TM by Midwest Microsystems). Thus, input parameters can be directly read/retrieved from data either routinely collected in commercial livestock operations or data generated by research projects. The initiative is carried forth by a consortium between Science Data Services (Dr. Simon Riedel), the German Institute for Tropical and Subtropical Agriculture [www.ditsl.org DITSL] (Dr. Christian Hülsebusch and Prof. Dr. Brigitte Kaufmann) and the University of Kassel (Dr. Uwe Richter, Prof. Dr. Eva Schlecht). The consortium appreciates the generous permission of the author, Dr. habil. Richard Baptist, to further develop his valuable tool with the aim to provide a flexible decision support tool for the management of livestock systems.
In a first step, the model was transcribed into a standalone application running under Windows XP/7 named PRY 3.0 beta – which can be downloaded here for test purposes
In a next step, a MySQL database will be coupled to PRY 3.0 beta that permits translation of CowSense (TM by Midwest Microsystems) export data into demographic input parameters for PRY.
DIC - Demographic Program Input Constants
Purpose of DIC
PRY provides an interactive routine for entering demographic parameters or inherent fitness traits. These are: survival rates, selective culling rates, age at first parturition, parturition interval and litter size. This routine is referred to as DIC (Demographic Program Input Constants). At every step of parameter entry, checks are carried out, error messages displayed and only consistent values accepted to avoid crashing of the simulation and derivation routines. Specification of age groups, rates and histograms is flexible. After entry, the parameters are formatted and saved to a work file from which they are later retrieved by the simulation and derivation routines.
Survival Rates
A survival rate is the fraction of animals still present at the end of a time interval if no living animal were disposed of. Such a rate represents an inherent potential and can be specified even for age classes which, in practice, are not at all represented because animals are culled before that age. Survival rates observed under a specific culling pattern may well differ from the survival rates to be specified as inherent demographic parameters. Survival rates can be specified for arbitrary age classes as either an annual rate or as a fraction surviving to the end of the specified interval. Such an interval or age class is defined in terms of a starting week or month of age and an ending week or month. The period covered can be more or less 8than a year.
Animals surviving to the ’biological’ maximum age specified, are assumed to be lost, rather than culled at the last time-step. However, animals surviving to a cull-for-age threshold lower than the ’biological’age limit,are assumed to be culled.
If only one survival rate per sex is specified, the age group then includes all ages from the first month or week of age up to the highest possible age. A maximum of 14 age groups can be defined. Male and female survival rates may be the same. However, age group boundaries and corresponding rates can also be defined for each sex separately.
Losses and culls in breeding females are not always clearly distinguishable. Emergency slaughter is an anticipated mortality or a cull, depending on the value of deadweight. Youngstock is never disposed of on voluntary grounds unless it has reached ’marketing’ age. Therefore, forced culls in youngstock are to be aggregated with losses. The value of deadweight can be adjusted correspondingly, to reflect an expected average of real losses of low salvage value and forced cullings of high salvage value.
SCRAP - Selective culling rates in breeding females
In practice, breeding females which have not yet reached the cull-for-age threshold are not culled on a yearly basis as assumed in most livestock productivity models. Rather, a certain fraction per parity can be expected to fail to conceive or pose problems like low yield or poor health. Culls based on problems like low yield or conformation are not really forced ones like culls for failure-to-conceive or poor health. Both forced and arbitrary culls of breeding females do, however, have the same effect in terms of population dynamics. That is why they are treated alike and aggregated into a ’selective culling rate per parity’ of breeding females (SCRAP-rate). For example, if the ’true’ sterility rate is 0.05 and the rate of low yielders is 0.10, the SCRAP-rate to be entered would be 0.15, which is the rounded value of the conditional probability:
1–(1–0.10) (1–0.05) = 0.145
assuming that an animal’s yield level is independent of its reproductive performance.
The SCRAP-rate should not include the fraction of lost animals, i.e., forced culls with a low enough salvage value to be aggregated with mortalities. The distinction is often made between involuntary and voluntary culls. The best way to avoid confusion is probably to first think in terms of animal losses, on the one hand, and culls on the other. Then, culls are further differentiated according to whether they are forced or arbitrary. It depends on the context of the modelling exercise how ’exits’ are partitioned among these categories.
’Sterile’ breeding females are assumed to be recognized as such only when a parturition is overdue. In the case of ’sterile’ nulliparous breeding females this means that they are culled at an age when practically all ’fertile’ age-mates have given birth. In the case of ’sterile’ primi- and multiparous animals it means that they are culled when fertile age-mates have nearly all given birth again. Animals with a low yield and animals of poor health are, like ’steriles’ likely to be culled only after weaning or at the end of a lactation when the parturition interval, statistically speaking, tends towards its end. Therefore, selective culls, both for failure-to-conceive and other ’problems’, are treated alike and assumed to take place shortly before the next parturition is due.
In conclusion, the compound rate of selective culling per parity is to give the fraction of breeding females in an age group which are earmarked to be culled when a next (or the first) parturition is ’overdue’. When culling actually takes place is detailed in the sections on the animal population emulator and the stationary-state demographic model, respectively. Both routines use the same parameter of a SCRAP-rate. The SCRAP-rate gives a fraction per parity. However, age dependency is taken into account by varying the rate by age. A minimum of two age groups and a maximum of 14 can be defined. The SCRAP-rate of the first age group is applied to nulliparous breeding females. The other rates are applied to those breeding females having a parturition in the respective age group. Like survival rates, SCRAP-rates are inherent parameters. An ’ear-marked’ breeding female can die or reach the cull-for-age threshold before ’scrapping’ actually takes place towards the expected end of the parturition interval.
Age at first parturition
The age at first parturition is specified in weeks or months. It is given as a frequency distribution. The special case of a histogram with only one column represents a statistical population with a mean but zero variance. As the column heights of the histogram are edited, the mean and standard deviation are calculated and displayed by the program. The histogram can be composed of up to 14 columns. The height of each column is entered using an arbitrary scale. It is not essential but preferable to specify a histogram with more than one column. With only one column very fluctuating population sizes will result for the dynamic model due to an effect of synchronisation. A multi-column histogram, even if it is the very crude approximation of a rectangular distribution, will desynchronize births. Consequently, simulated population sizes and structures become more continuous.
Parturition interval
Like age at first parturition, the parturition interval is specified as a histogram. The remarks of the preceding paragraph concerning age at first parturition apply. The parturition interval represents only a partial aspect of reproductive fitness. In the model, it is complemented by the SCRAPrate which normally represents an age-dependent sterility rate.
Litter size
Litter size is specified as the histogram of number-of-young per litter. An average litter size which is not an integer number cannot be specified as a single-column histogram. A multiplecolumn histogram with integer class means must be defined so as to get an appropriate population mean. This weighted average is continuously updated and displayed as the histogram of litter size is edited. Even when average litter size can be given as an integer value, it is preferable to enter a multiple-column histogram, in order to smoothen fluctuations of population size in runs of the dynamic model.
APE - Animal Population Emulator
Purpose of APE
The Animal Population Emulator (APE) stochastically simulates births, culls and losses in a seed herd or flock of finite size (¡1000). APE can only simulate population dynamics but not productivity proper. The procedure can be used to analyse population structure and animal offtake over time. This can be a useful complement to stationary-state demography, especially with regard to financial discounting exercises. APE is an ’electronic’ population system. Whether it can model animal populations depends on the objectives. Many aspects of livestock populations are idealised or abstracted from. For example, litter size is assumed to be the same in different parities. Culling regime and fitness traits remain the same over time. Due to the stochastic variation of survival, sex-ratio, age at first parturition, calving interval, litter size and culling, every simulation run will give different results. Apart from being a dynamic and stochastic system, APE models reproduction, losses and culls in much the same way as does the deterministic Stationary-state Animal Demographic Model (SAM, see below). Consequently, APE can be used to validate SAM and vice versa.
Index card population
An individual animal is represented by a file record whose entries represent the sex of the animal, its age in time units of weeks or months, an identification number, the time elapsed since the last parturition (if applicable), and the number of weeks or months to wait until the next parturition, provided the animal survives. Records of females ’earmarked’ for selective culling, indicate that there is no next parturition even if the animal survives. There are no entries regarding yields.
At consecutive time-steps (weeks or months) each survivor’s record is either eliminated or maintained. At the beginning of a time-step, the program looks up the survival probability for the week or month corresponding to the animal’s age and decides over survival or loss of the animal on the basis of a random number. If a female survives, the program looks up whether a parturition is due. If so, litter size is determined by generating a random integer number from a distribution as specified by the histogram of litter size. The sex of each animal born is randomly determined with an expected frequency of males of 50 %. For newborn females the SCRAPrate of nulliparous females randomly determines whether the animal is to have a first parturition. If it is not to be sterile, the number of time units to wait until the animal’s first parturition (if it survives), is drawn from a frequency distribution defined by the histogram of age at first parturition.
For the females having given birth, the SCRAP-rate specified for their agegroup randomly determines whether a next parturition is expected. If so, the number of time units to wait is drawn from a frequency distribution defined by the histogram of the parturition interval. After thus simulating mortalities and reproduction, culling decisions are taken. APE offers seven different options which are explained below in the section on the simulation plan. Before a next time-step starts, the age entries of the survivors are updated. Cycles are repeated until the population dies out or grows too big (>1000), until run-time is out or until the required number of repetitions and of time-steps per repetion are done. A repetition resumes simulation starting off again with the same seed herd or flock. At the end of the simulation experiment the surviving population of animal records is saved in a work file. This population of survivors can be used as a seed herd or flock in subsequent simulation runs.
Seed herd or flock
APE needs a seed herd or flock. It can consist of up to 1000 animals. When the seed population is entered the sex of the animal and its age have to be specified. Nulliparous females have to be identified as such. For primi- or multiparous females a specification of the time elapsed since their last parturition is required. Animals having identical entries are entered as multiple copies of a record.
After at least one simulation run, a work file is saved containing the population of survivors from the final time-step of the completed simulation experiment. This population of records contains the same entries as the records of a seed herd or flock. Such a population of survivors can therefore serve as a seed population of a subsequent simulation experiment. This 13feature can be used to vary parameters over time.
The population of survivors can be edited before it is used as a seed population. Editing can consist of a random reduction of population size, or a random increase. It is also possible to ’manually’ select animals and eliminate them from the population. Culling patterns not covered by the options offered can be simulated step-wise, by loading the (ASCII) file of survivors into a spreadsheet or database package and by using standard procedures like sorting, selecting and deleting, to eliminate groups of records before saving the edited file back to the work file containing the seed population. The specification, in that file, of the number of records it contains, has to be updated before saving. The cropped population is then left to develop over one or more time-steps before it is cropped again.
Simulation plan
Before the seed population can be developed, a work file containing a simulation plan has to be edited. The simulation plan specifies an experimental design and the culling pattern to which the seed population is to be subjected. The experimental design specifies whether the seed population is a previously entered one, or whether it consists of survivors from a preceding run. It also decides on the number of repetitions to be run, the number of time-steps to be simulated per repetition and the length in number of time-steps of an accounting interval, i.e., the period over which the numbers of culls, deaths, births and survivors per animal category are to be cumulated before sub-totals are saved. In addition, the program prompts for a maximum run-time after which the experiment is stopped if it is not yet completed. As a further condition to stop a repetition, the maximum population size has to be specified.
To define the culling pattern, one of seven optional practices has to be selected:
- No culling, only natural deaths until target population size is reached or run-time is out
- Culling only when target population size is exceeded
- Constant offtake rate whether the population grows or decreases
- Allowance for a constant rate of increase in population size
- Immediate disposal of newborn males; all females are bred until they are culled for sterility or lost
- All newborn females become potential breeders culled at an age threshold or when sterile
- A fixed number of male and female breeding animals is kept whose age exceeds the youngstock disposal age but is below a cull-for-age threshold
For some of these options (2, 3 and 4), additional specifications are prompted. When one or more animals have to be culled, a decision has to be taken as to which animal(s) from among the survivors has to be eliminated. APE simulates four optional strategies:
- Each animal’s entries are displayed for a culling decision.
- A culling rank is determined for each animal. Old males have highest culling priority. Females are ranked according to ’fertility’ (i.e., time units that have elapsed since the last parturition) and age. ’Sterileyoung’ is culled before ’fertile-old’. During culling, minimum requirements are considered. If no sufficiently old or ’sufficiently sterile’ animals are left, males are eliminated starting with the oldest ones. When no males are left, females which in principle are too young or too ’fertile’ are culled according to the established ranking.
- Ranks are established similarly. However, ’fertile-old’ females are culled before ’sterile-young’ females.
- Basic pattern as under option 2. However, when no ’sterile’ females are left, sexually immmature ones with minimum age requirement are culled. After elimination of males, immature females are culled in reverse order of ages, i.e., youngest first.
Minimum requirements sometimes are conflicting and cannot all at the same time be taken into account when many animals have to be culled in order to keep population size constant. The number of violations are recorded with the results. Culling option 7 avoids this kind of conflict and is the most relevant in a stockbreeding context.
Demograms
Over the length of the ’accounting’ period specified in the experimental design, losses and culls are cumulated for the six animal categories specific to APE, i.e., adult and subadult males, adult and subadult females with either no or at least one parturition. The sub-totals per category are saved in a work file for successive ’accounting intervals’ within a repetition. Annualized rates of births, culls and losses are shown, as well as the population growth rate. The base for these rates is not population size at the start or the end of the ’accounting’ interval but, rather, the average size over the length of the ’accounting’ interval. Population structure is expressed as the number of animals still alive at the end of a period in each of the six animal categories.
Results are saved in an ASCII work file. If an experimental design specifies 3 repetitions with 5 periods each, the work file will contain 15 records at the end of the completed experiment. In addition to the 15 data records the work file contains a record with the abbreviated variable names or column headers. For graphical or statistical analyses, variable names and data from the work file of results have to be imported into a spreadsheet. Within the spreadsheet, the results can be sorted, aggregated or plotted, and statistics can be calculated.
A standardized form of presenting population dynamics has been suggested and referred to as a demogram. A representative demogram is reproduced in Figure 3 (will be inserted) which is an example of how simulation results can be presented in order to reveal the development over time of population size, population structure, animal offtake, offtake composition and demographic rates.
SAM - Stationary-State Animal Demographic Model
Purpose of SAM
The Stationary-State Animal Demographic Model (SAM) derives population structure, animal offtake, a number of life expectancies and the potential rate of increase of population size for an infinitely large population at the stationary-state equilibrium of the imposed culling regime. Growth is zero because females not needed to replace lost or culled breeding females, are ’fattened’, or rather, ’sized’. The program automatically varies disposal ages to indicate how this affects stationary-state demography. Disposal age of female surplus and male youngstock, respectively, is varied in increments of one quarter of the age at first parturition. Simultaneously, the cull-for-age threshold of breeding females is varied in increments of the parturition interval. The effect of varying SCRAP-rates can be analysed by running SAM with previously modified rates.
Life and fecundity tables
Stationary-state demography is derived from life, fecundity and auxiliary tables generated according to actuarial principles applying elementary probabilistic calculations. The required tables are automatically generated by SAM on the basis of the demographic input constants, i.e., the inherent fitness traits of a population. A life table is a vector of weekly, monthly or annual survival rates. A fecundity table gives the number of young produced per surviving female at various ages. The set of vectors as generated by SAM is referred to as actuarial table. Table 10 represents such a set derived from the fitness traits in Table 9. The population could be a laboratory strain of not very viable guinea pigs. The actual values used are quite irrelevant because they only serve to exemplify the actuarial method.
TABLE 9 - Fitness traits assumed for a hypothetical example of laboratory guinea pigs comming soon
TABLE 10 Actuarial table generated generated for the example of laboratory guinea-pigs comming soon
Life expectancies
Table 11 shows some of the life expectancies which SAM calculates for the example of guineapigs. Thecull-for-age threshold of breeding females is 18 or 14 months. The upper level rep- resents the ’biological’ maximum age.
Breeding females are only culled when sterility is recognized but otherwise they are kept until they are lost. The few who might reach the maximum age die. At a cull-for-age threshold of 14 months the population’s viability is reduced, which is reflected by the reduction from 1913% of the potential rate of increase of population size (see below). A further reduction of the cull-for-age threshold from 14 to 10 months makes the population unviable and a stationarystate is not possible at this level.
Potential rate of increase of population size
A stationary state can only exist when the population is sufficiently viable to maintain itself despite losses and culls. A measure of population viability is the potential rate of increase of population size. It reflects the rate of increase expected when culling of fertile females is completely suppressed and when the population has established an equilibrium with regard to structure and steadiness of growth. The derivation of this rate from the actuarial table is not trivial. It requires an iterative solution of Lotka’s equation. The program needs only about four to six iteration 18 cycles to find the approximate rate for which the right-hand side of Lotka’s equation deviates by less than 0.0001 from the expectation of unity.
The potential rate of increase of population size may be found to be negative. This means that the closed population is bound to die out gradually. This can be caused by too heavy culling of breeding females (SCRAP-rate), or because the cull-for-age threshold is too low, or because of weak inherent fitness. In such cases further derivations have to be suppressed because a stationary-state is not possible. Thus, the calculation of the potential rate of increase of population size is a safeguard against unrealistic assumptions and serves as a consistency check with regard to assumed fitness values and imposed culling pressure.
TABLE 11 - Life expectancies under two regimes with different cull-for-age thresholds for breeding females of laboratory guinea-pigs
No culling for age (threshold set to maximum biological age)
- Life expectancy at birth (years of age) of breeding females : 0.8230
- Life expectancy at birth (no. of parturitions) of bdg. fems. : 1.1416
- Number of female surplus per newborn female : 0.1416
- Avg. age at parturition in years (gen.int. for breeding females): 0.6684
- Potential annual rate of increase of population size (%) : 19.40
- Selective culls in % of breeding female offtake : 100.00
- Cullings for old age in % of bdg female offtake : 0.00 item Breeding
- Female offtake / Breeding Female losses : 0.40
- Cull-for-age threshold set to 14 months
- Life expectancy at birth (years of age) of breeding females : 0.7916
- Life expectancy at birth (no. of parturitions) of bdg. fems. : 1.0955
- Number of surplus females per newborn female : 0.0955
- Avg. age at parturition in years (gen.int. for breeding females): 0.6410
- Potential annual rate of increase of population size (%) : 13.47
- Selective culls in % of breeding female offtake : 75.24
- Cullings for old age in % of bdg female offtake : 24.76
- Breeding Female offtake / Breeding Female losses : 0.66
TABLE 12 - Offtake rate, composition and population structure under two regimes with different cull-for-age thresholds for the example of laboratory guinea-pigs
No culling for age (threshold set to maximum biological age):
comming soon
Offtake rate and population structure
Table 12 shows that the cull-for-age threshold of 14 months increases all offtake rates relative to those at 18 months. At each cull-for-age threshold, different combinations of disposal ages of youngstock produce different offtake rates, offtake compositions and population structures. An increased offtake rate is, of course, not an advantage in itself. Other offtakes, their unit values and the feed requirement involved have to be taken into account. This is accomplished by the program components FOC and BOI described in later sections.
PIC - Produce-Related Program Input Constants
FOC - Find optimal Culling Ages
Bio Breakdown of Offtakes and Intake
The Algorithms
Before you Start
Hardware Requirements
| System Architecture | This system runs on 32 and 64bit Systems |
| Operation System | Microsoft Windows |
| Win Version | Win 7, Win 8, Win 10 |
| HDD Space required | 300MB |
| RAM | 2 GB (4 Recommended) |
| Misc | Requires the Installation of some Database-Modules from Microsoft |
Download
Unless you are a developer or require Modules from the original DOS Software, you most proably want to use the 3.x Version of the Software, provided as an installable Windows App. Download of other Versions below
PRY 3.x
Latest Version
| Version | File | ReleaseNotes |
|---|---|---|
| 1.0.13 | PRY 3.0.12 Windows Installer | abcdef.txt |
Access previous Versions of PRY
Installation Manual
| Requirements | |
| What | Description |
|---|---|
| PRY Installer | Get the PRY Zip File (here) |
| Unzip Software | WinRar, WinZip or 7zip - you most probably have such Software on your computer |
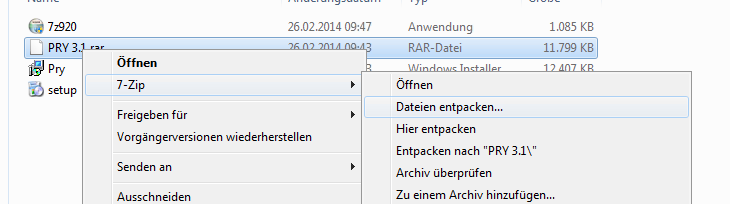
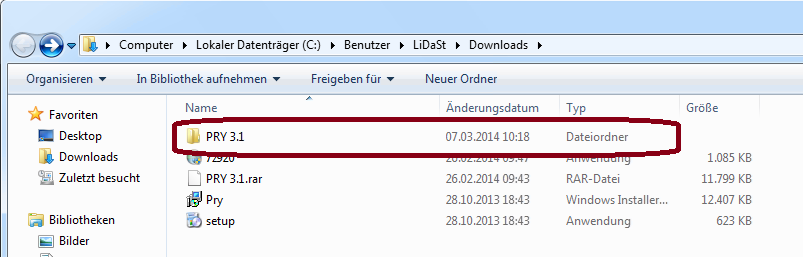
1.) Extract the Zip File into any Folder
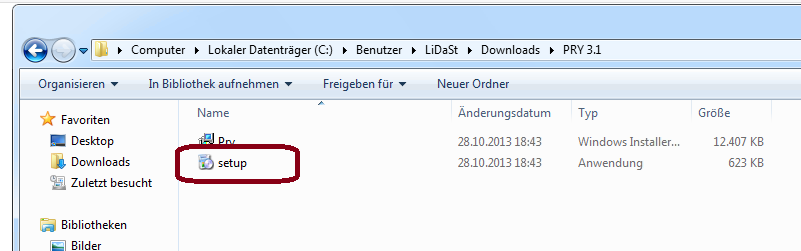
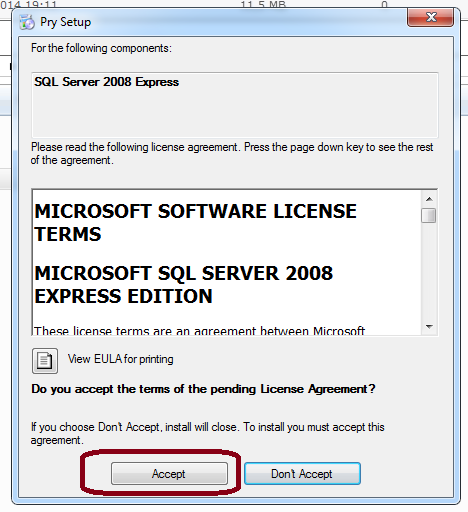
2.) Open the Folder and click on "Setup.exe"
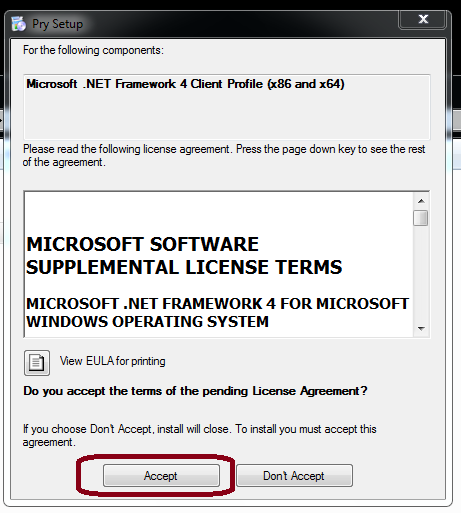
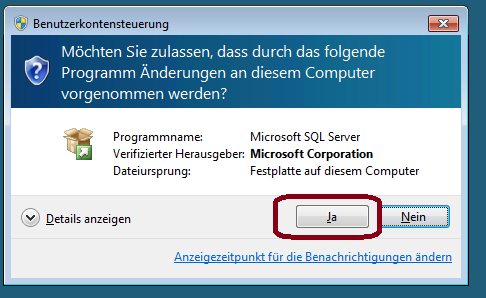
3.) Two modules will be directly downloaded from Microsoft - if you don't already have them installed on your computer, you need to agree to the Terms and Conditions and follow the installation instructions of those modules
4.Allow Microsoft to install Modules on your Computer
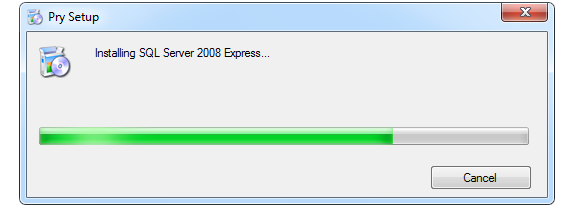
5. The installation is in process
PRY' is now successfully installed on your Computer. You will find a Link to the Software on your Desktop (Icon is black, so you might not see it directly when your Background is black) and in the Start-Menue.
If you encounter any problem with installing PRY on your computer, you may ask for support
User Manual
For other Versions see User Guide here
- Version 2.x
- PRY realized as Modules in an Excel sheet
- Version 1.x
- The original PRY, a DOS console Program
Model Input Parameters
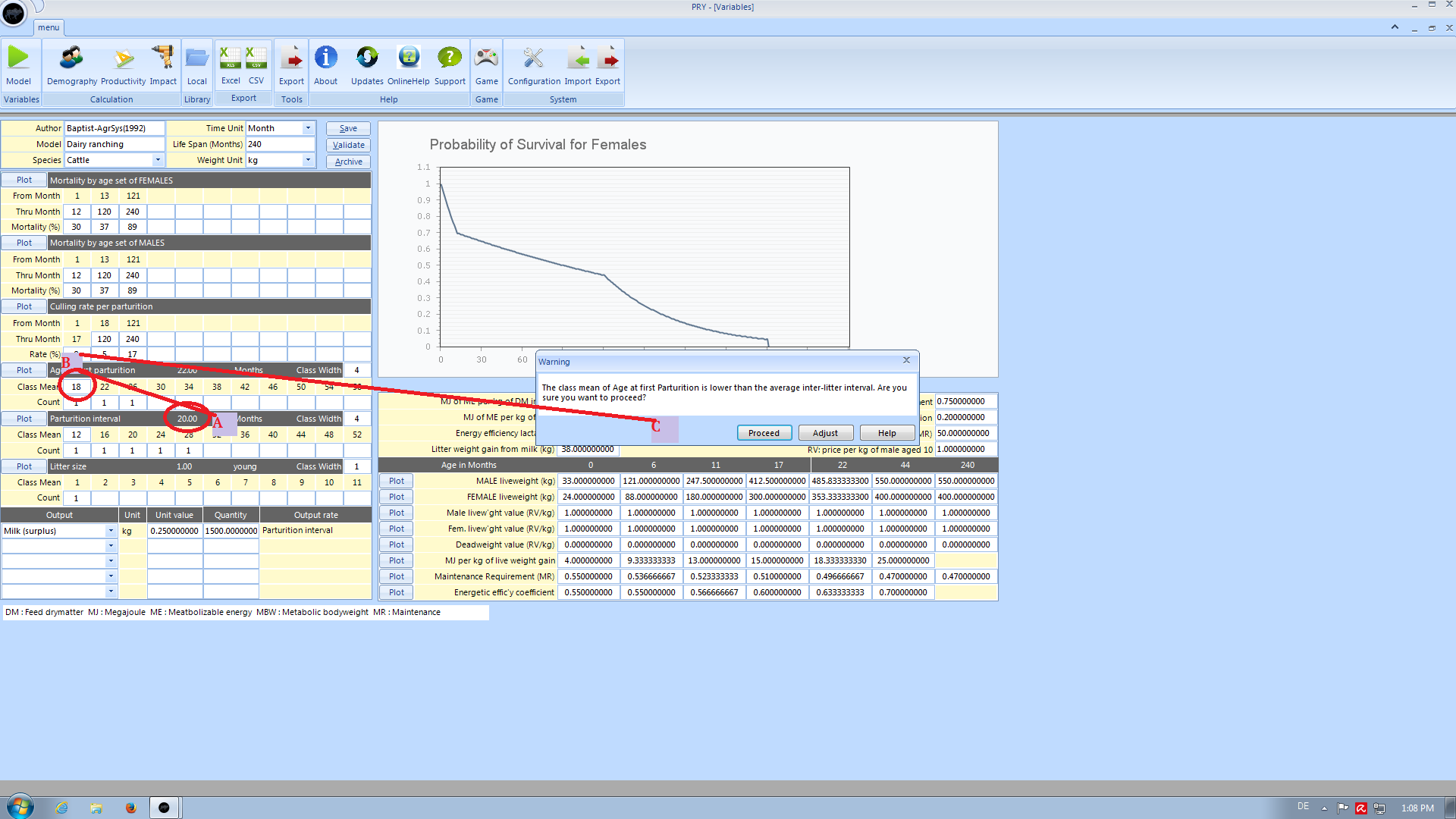
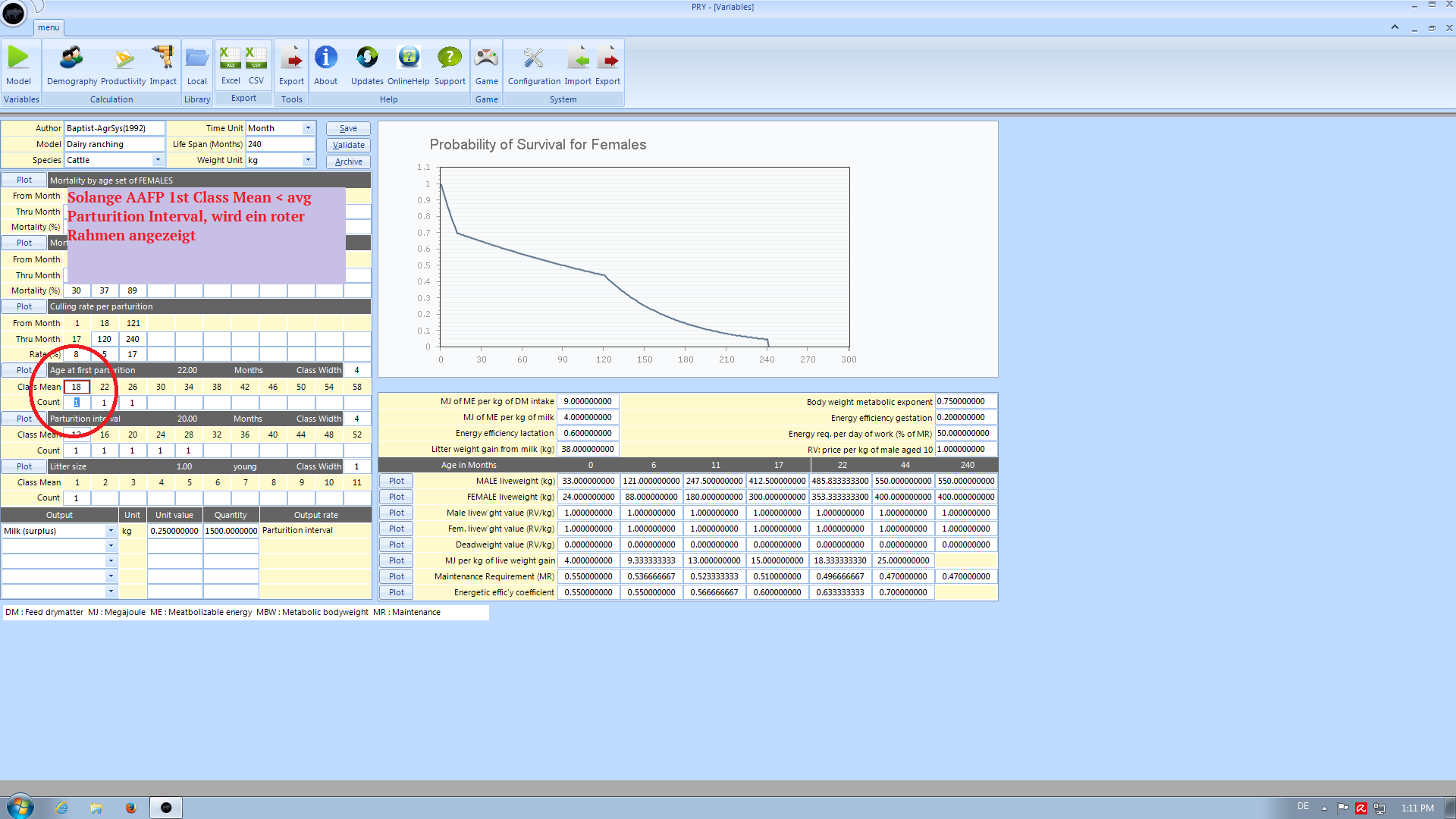
Age at first Parturition
When a class mean in the first class of age at first parturition is entered which is below the average inter-litter interval, a warning shows up to recheck your values. You have three options:
- Proceed and leave your input as it is
- Correct your value
- Click the Help Button to learn why this value might be critical for your model
Technical Documentation
Literature
Many studies have been conducted by using the PRY Software. We are trying to collect all, so if you know of any further study, let us know, we will list them here. If you have any questions about those publications, you may contact DITSL , visit the [contact] page for further details.
Herd Analysis with PRY
| Author | Year | Journal | Title | Link/File | Species |
|---|---|---|---|---|---|
| Baptist,R. Sommerlatte | 1992 | Small Ruminant Research | Evaluation of cropping strategies in game ranching using a livestock productivity model | http://dx.doi.org/10.1016/0921-4488(91)90124-9 | Game |
| Fink H. and Baptist R. | 1992 | Better feeding for improved production - FAO Series | Herd dynamics modelling applied to a venison ranch in Kenya | http://www.fao.org/docrep/u8750t/u8750T04.htm | Game |
| Anonymous | 1995 | Wildlife and Nature | Herd Dynamics modelling applied to a Venison ranch in Kenya | Game | |
| Fink | 1990 | unpublished (Diploma Thesis) | Schätzung demographischer Parameter in der Wildnutzung aus ermitteltem Propulationswachstum und -struktur, Entnahmerate und Zusammensetzung der Entnahme auf einer kenyanischen Wildranch | DOI | Game |
| Kaufmann, B. | 199x | contact | Cattle/Camel | ||
| Huelsebusch, C. | 199x | contact | Cattle/Camel | ||
| Dos Santos / Neuzling, A. | 200x | contact | Cattle | ||
| Dickhoefer et al. | 2012 | Agricultural Systems 110,C, 131-141 | Modeling herd development and revenues from Jabal Akhdar goats under current and intensified management | http://www.sciencedirect.com/science/article/pii/S0308521X12000583 | Goat |
| Riedel et al. | 2014 | Livestock Science, 160, 151-162 | The productivity of traditional smallholder pig production and possible improvement strategies in Xishuangbanna, South Western China | http://www.livestockscience.com/article/S1871-1413%2813%2900502-7/abstract | Pigs |
| Hofsommer | 2014 | contact | Cattle | ||
| Aufderheide, M. | 2014 | contact | Cattle | ||
| Wario, H.T. | 2015 | Social Ecological Research Series | An integrated assessment of resource use strategies in the Borana pastoral system of southern Ethiopia | http://d-nb.info/1075658810/34 | Cattle |
Methodology
| Author | Year | Journal | Title | Link/File |
|---|---|---|---|---|
| Baptist, R. | 1987 | Agricultural Systems | Computer Simulation of Monitoring Herd Productivity under extensive Conditions: Sampling Error of Herd Size and Offtake Rate | http://dx.doi.org/10.1016/0308-521X(87)90003-5 |
| Baptist, R. | 1988 | Agricultural Systems | Herd Flock Productivity Assessment using the Standard Offtake and the Demogram | http://dx.doi.org/10.1016/0308-521X(88)90022-4 |
| Baptist, R. | 1991 | unpublished | PRY Manual | |
| Baptist, R. | 1992 | Habilitation | Population Dynamics and Productivity at the stationary State of Culling Regimes in Livestock Herds and Flocks | |
| Pittroff and Cartwright | 2002 | Arch. Latinoam. Prod. Anim. | Modeling livestock systems. I. A descriptive formalism | http://www.alpa.org.ve/PDF/Arch%2010-3/Archivos10(3)193.pdf |
| Rushton, J. | 2009 | CABI Publishing | The Economics of Animal Health and Production , p. 96 | ISBN 1845931947 |